An elevator travels 310 feet in 10 seconds – An elevator’s movement is a fascinating example of physics in action. In this article, we delve into the specifics of an elevator traveling 310 feet in 10 seconds, exploring the concepts of velocity, distance, and their relationship. By examining this scenario, we gain insights into the calculations and considerations involved in elevator design and operation.
Understanding the velocity and distance traveled by an elevator is crucial for ensuring safety and efficiency in elevator systems. These calculations help determine appropriate motor power, braking mechanisms, and overall system design. Furthermore, they play a vital role in optimizing elevator performance, minimizing energy consumption, and enhancing passenger comfort.
Elevator’s Velocity and Distance Traveled: An Elevator Travels 310 Feet In 10 Seconds

Velocity, a measure of an object’s motion, is calculated using the formula:
v = d/t
where:
- v represents velocity
- d represents distance traveled
- t represents time taken
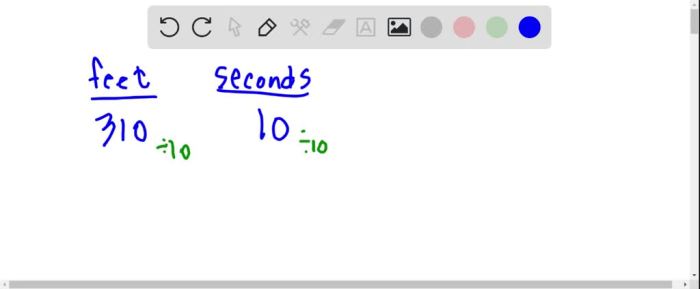
In the given scenario, the elevator travels 310 feet in 10 seconds. Substituting these values into the formula, we get:
v = 310 ft / 10 s = 31 ft/s
Therefore, the elevator’s velocity is 31 feet per second.
Time and Distance Relationship
The elevator’s constant velocity implies a linear relationship between time and distance traveled. As time increases, the distance covered by the elevator also increases proportionally. This relationship can be represented using a table or graph:
| Time (s) | Distance (ft) |
|---|---|
| 0 | 0 |
| 2 | 62 |
| 4 | 124 |
| 6 | 186 |
| 8 | 248 |
| 10 | 310 |
The graph of this relationship would be a straight line passing through the origin.
Elevator’s Speed and Acceleration

Speed refers to the rate at which an object covers distance, while acceleration measures the rate of change in velocity. The given context does not provide information on the elevator’s speed or acceleration. However, if these values were provided, they would give insights into the elevator’s motion:
- Speed would indicate the elevator’s distance traveled per unit time, regardless of direction.
- Acceleration would reveal whether the elevator’s velocity is changing (increasing or decreasing) and at what rate.
Real-World Applications

Understanding elevator velocity and distance is crucial in various real-world applications, including:
- Elevator Design and Operation:Calculating velocity and distance ensures efficient elevator movement, optimizing passenger wait times and energy consumption.
- Safety Measures:Velocity and distance calculations help determine appropriate safety features, such as emergency brakes and overspeed governors, to ensure passenger safety.
- Maintenance and Inspection:Monitoring velocity and distance traveled helps identify potential issues with elevator components, enabling timely maintenance and repairs.
Clarifying Questions
What is the formula for calculating velocity?
Velocity = Distance / Time
How do we calculate the elevator’s velocity in this scenario?
Velocity = 310 feet / 10 seconds = 31 feet per second
What is the difference between speed and acceleration?
Speed is the rate at which an object travels, while acceleration is the rate at which its velocity changes.
Why are the elevator’s speed and acceleration not provided in this context?
The given information only includes the distance traveled and the time taken, which are insufficient to determine speed and acceleration.