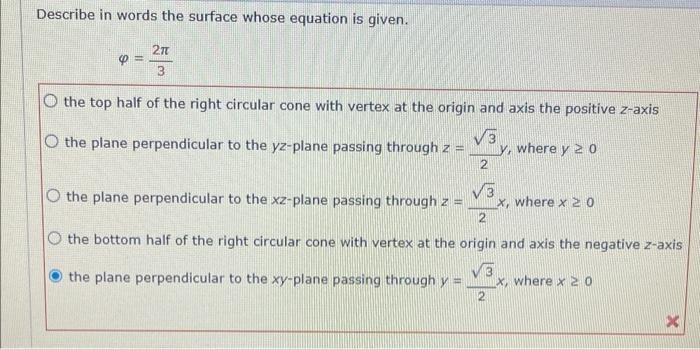
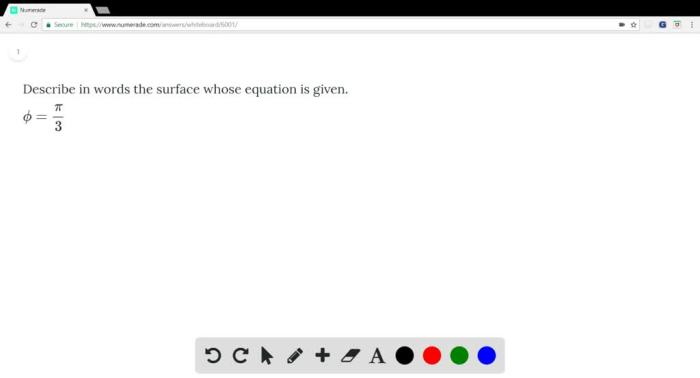
Describe in words the surface whose equation is given. – Embark on a journey into the realm of surfaces, where equations hold the key to unlocking their enigmatic forms. Describe in words the surface whose equation is given, unraveling the intricacies of its geometry through a captivating exploration of its defining characteristics and applications.
Surfaces, ubiquitous in nature and technology, present a fascinating canvas for mathematical exploration. From the gentle curves of a leaf to the intricate folds of a protein, understanding the language of surfaces empowers us to decipher the world around us.
Surface Equation Basics: Describe In Words The Surface Whose Equation Is Given.

A surface equation is a mathematical equation that describes a surface in three-dimensional space. Surface equations can be used to represent a wide variety of surfaces, including planes, spheres, cylinders, and cones. There are three main types of surface equations: implicit equations, parametric equations, and vector equations.
Implicit equations are equations that define a surface as the set of all points that satisfy the equation. For example, the equation of a sphere with radius rcentered at the origin is x2+ y2+ z2= r2.
Parametric equations are equations that define a surface as the set of all points that can be reached by varying a set of parameters. For example, the parametric equations of a sphere with radius rcentered at the origin are x= rcos( u)sin( v), y= rsin( u)sin( v), and z= rcos( v), where uand vare parameters that vary over the range 0 ≤ u≤ 2π and 0 ≤ v≤ π.
Vector equations are equations that define a surface as the set of all points that can be reached by adding a vector to a given point. For example, the vector equation of a plane with normal vector nand passing through the point pis r= p+ tn, where tis a parameter that varies over the real numbers.
Describing Surfaces in Words

Surfaces can be described in words using a variety of terms, including shape, size, orientation, and texture. The shape of a surface is determined by its curvature. A surface with positive curvature is curved outward, like a sphere. A surface with negative curvature is curved inward, like a saddle.
A surface with zero curvature is flat, like a plane.
The size of a surface is determined by its area. The area of a surface can be calculated using a variety of methods, including integration and the surface integral. The orientation of a surface is determined by its normal vector.
The normal vector is a vector that is perpendicular to the surface at every point. The texture of a surface is determined by its roughness. A rough surface has a lot of small bumps and indentations, while a smooth surface has few.
Surface Characteristics
Surfaces have a variety of characteristics that can be used to describe them. These characteristics include shape, size, orientation, and texture.
The shape of a surface is determined by its curvature. A surface with positive curvature is curved outward, like a sphere. A surface with negative curvature is curved inward, like a saddle. A surface with zero curvature is flat, like a plane.
The size of a surface is determined by its area. The area of a surface can be calculated using a variety of methods, including integration and the surface integral.
The orientation of a surface is determined by its normal vector. The normal vector is a vector that is perpendicular to the surface at every point.
The texture of a surface is determined by its roughness. A rough surface has a lot of small bumps and indentations, while a smooth surface has few.
Surface Representations
Surfaces can be represented in a variety of ways, including implicit equations, parametric equations, and vector equations.
Implicit equations are equations that define a surface as the set of all points that satisfy the equation. For example, the equation of a sphere with radius rcentered at the origin is x2+ y2+ z2= r2.
Parametric equations are equations that define a surface as the set of all points that can be reached by varying a set of parameters. For example, the parametric equations of a sphere with radius rcentered at the origin are x= rcos( u)sin( v), y= rsin( u)sin( v), and z= rcos( v), where uand vare parameters that vary over the range 0 ≤ u≤ 2π and 0 ≤ v≤ π.
Vector equations are equations that define a surface as the set of all points that can be reached by adding a vector to a given point. For example, the vector equation of a plane with normal vector nand passing through the point pis r= p+ tn, where tis a parameter that varies over the real numbers.
Surface Applications
Surfaces have a wide variety of applications in a variety of fields, including engineering, architecture, and computer graphics.
In engineering, surfaces are used to model the shape of objects, such as cars, airplanes, and buildings. Surfaces can also be used to analyze the stress and strain on objects.
In architecture, surfaces are used to design the shape of buildings and other structures. Surfaces can also be used to create interesting and visually appealing effects.
In computer graphics, surfaces are used to create 3D models of objects. Surfaces can also be used to create realistic textures and lighting effects.
User Queries
What is the purpose of describing surfaces in words?
Describing surfaces in words helps us to understand their shape, properties, and behavior. It enables us to communicate about surfaces effectively and to convey their characteristics to others.
How do we describe surfaces in words?
Surfaces can be described using various elements such as their curvature, smoothness, and boundaries. We can also use geometric terms like planes, spheres, and cylinders to approximate their shape.
What are some applications of surface description?
Surface description finds applications in fields such as architecture, engineering, computer graphics, and manufacturing. It helps us to design and analyze objects, create realistic 3D models, and understand the behavior of surfaces under different conditions.